Diamond effect: Hearts, arrows, and bow ties
By Mike Botha, RS, Master Diamond Cutter
At first glance, this article’s title might sound oxymoronic, as arrows may seem antithetical to bow ties; a closer look, however, reveals a profound resemblance.
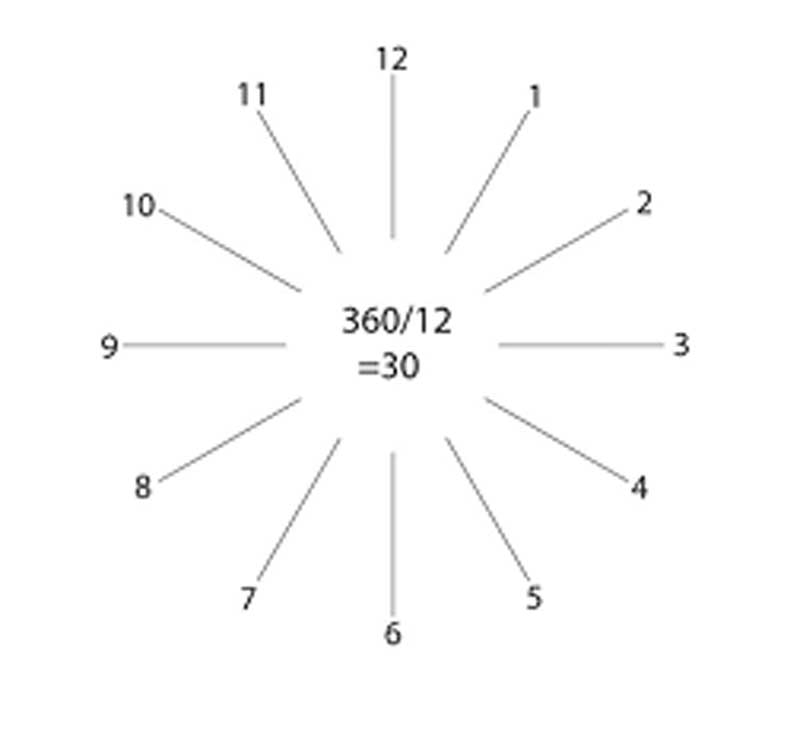
Image courtesy Embee Diamond Technologies
Indeed, when the crown and pavilion facets on a round brilliant diamond are in alignment (i.e. same index) and are at similar angles for the respective opposing facets, what could be seen in the pavilion of the diamond (when viewed from the crown) are eight arrows. Any deviation in angles and indices within a facet group would have a visible effect on the symmetry of these arrows.
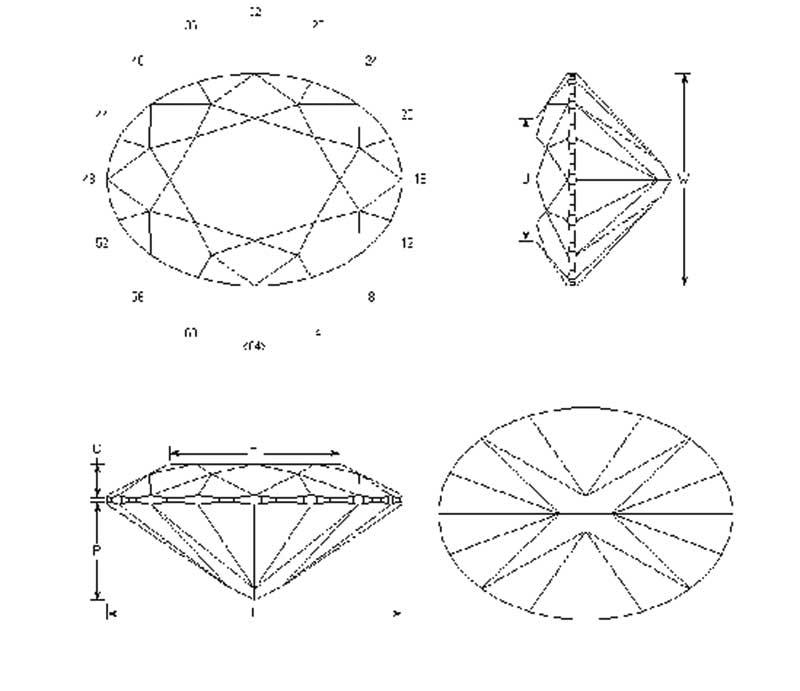
To understand this better, we need to explore the geometry of polished diamonds (i.e. round brilliant), particularly the placement of facets and their respective angles. It should be the objective of any cutter to obtain maximum angular variance between facets. With this in mind, we must differentiate between angles (radial position) and angles (inclination to the table).
Necessary details
‘Facet definition’ is determined by the index (radial) and angular positions of facets; ‘index’ (radial position or first element of facet definition), meanwhile, refers to the radial position of facets.
As an analogy, consider a clockface (Figure 1), which is divided into 12 equal parts. Because there are 12 numeral positions, it follows logic that numerals are positioned in 30-degree increments (or: 360 divided by 12). The numerals, therefore, represent their radial positions on the dial. If ‘12’ is the datum (reference), ‘1’ would be 30 degrees, ‘2’ would be 60 degrees, and so forth.

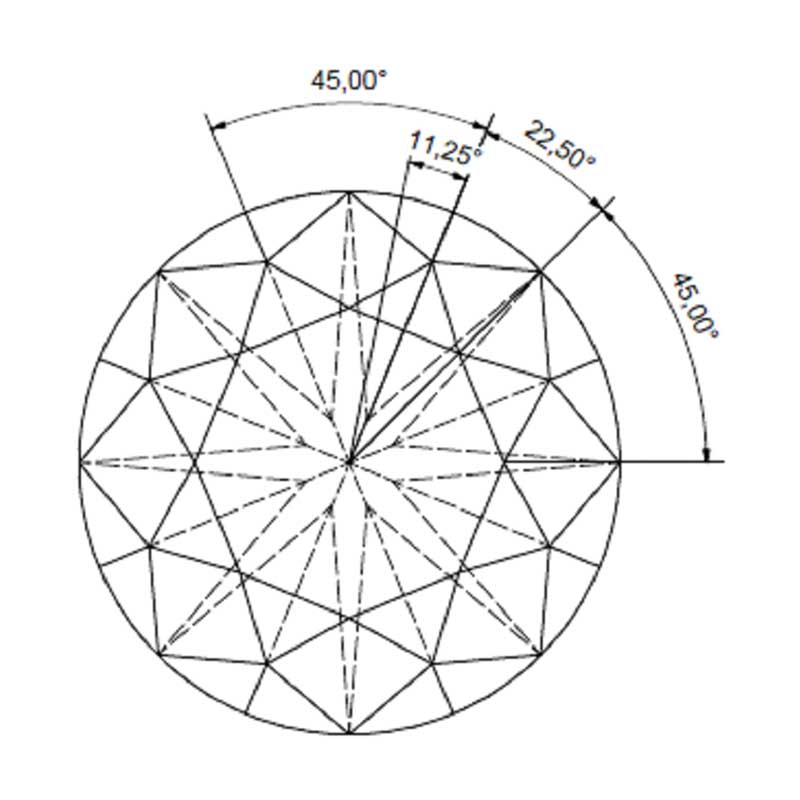
In diamonds, radial positions (facet definition) are expressed in multiples of 11.25 degrees (or: 360 divided by 32). To illustrate this, think of a pizza (Figure 2).
Consider:
- If a pizza is cut in half, the pie will have two segments (or slices) of 180 degrees each.
- If the pie is quartered, it will have four segments of 90 degrees each.
- If the four quarters are divided again, the pie will have eight segments of 45 degrees each.
- If those eight are divided again, the pie will have 16 segments of 22.5 degrees each.
- If the sections are divided one more time, it will have 32 segments of 11.25 degrees each.
Now, interestingly, we have a picture resembling the segments of a round brilliant diamond.
On a round brilliant, all the facets relate to one another in a radial position for a minimum of 11.25 degrees (or multiples of 11.25 degrees—i.e. 11.25 x 2 = 22.5 degrees, 11.25 x 4 = 45 degrees, etc.) on a well-cut diamond.
The facet definition of a round brilliant is, therefore, a minimum of 11.25 degrees, seen in a radial context (Figure 3).
Angle
Images courtesy Embee Diamond Technologies
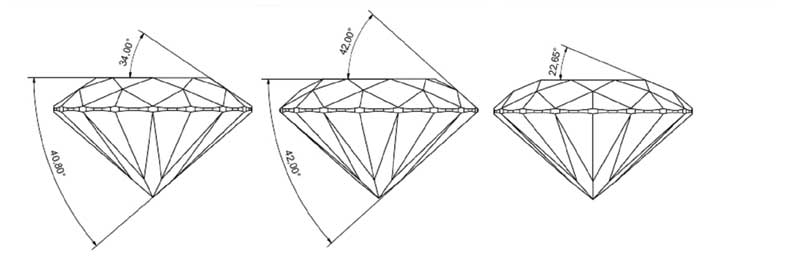
Angle refers to the inclination of facets in relation to the table facet. The table facet is the datum (reference) for the angles of the facets. Typical angles for well-defined arrows in round brilliant diamonds can be seen in Figures 4 to 6.
Returning to the arrows
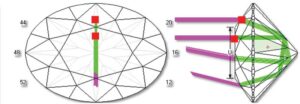
The arrows observed on well-cut round brilliant diamonds are an optical phenomenon, whereby the head of the viewer obscures the high-angle light that should be reflected by the diamond.
The American Gem Society (AGS) Angular Spectrum Evaluation Tool (ASET) and the Ideal-Scope are examples of tools able to capture this behaviour in an effective way.
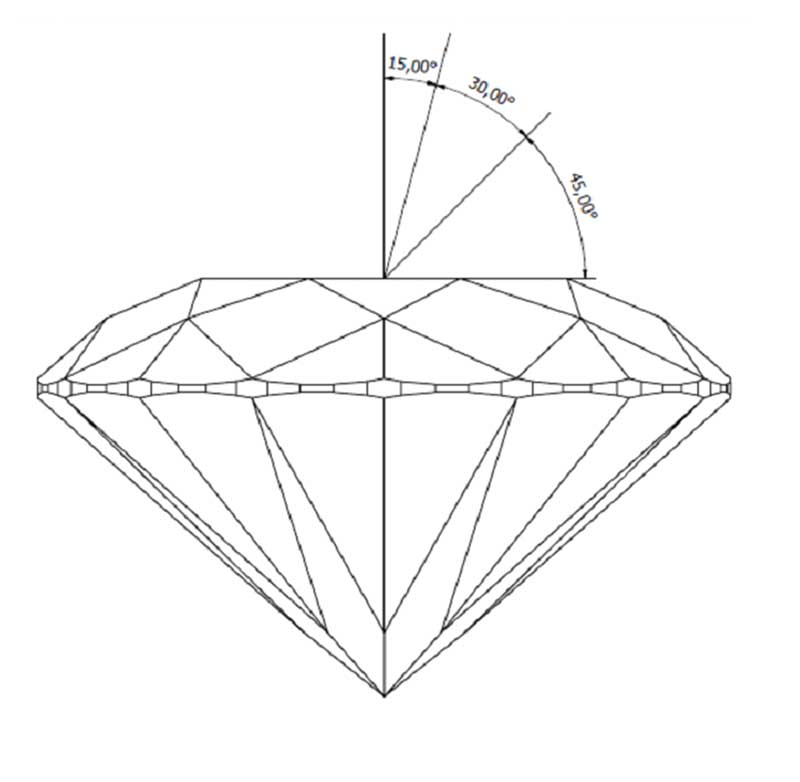
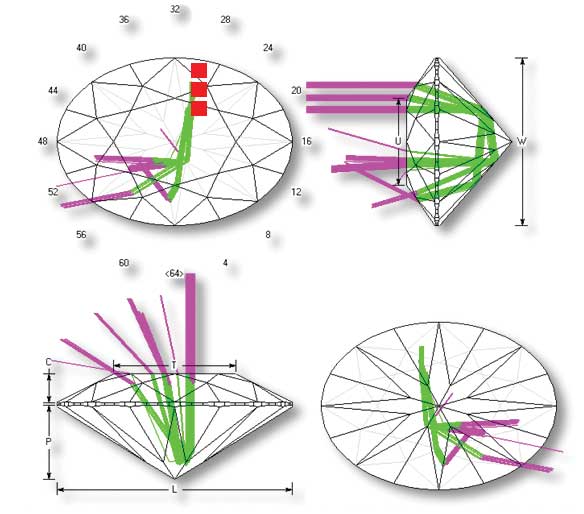
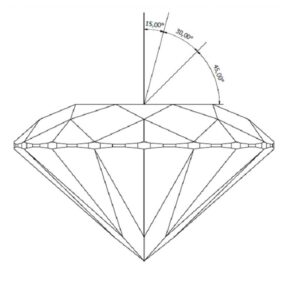
To expand this a bit further, one must look at the diagram of a round brilliant (Figure 7): as depicted, light that reaches the diamond within the (approximate) 15-degree vector would normally be obscured by the head of the viewer. (I say ‘approximate’ because this degree could be greater if the viewer has big coiffure.)
This vector is typically rendered as blue. The next vector (30 degrees) is referred to as high-angle light and rendered as red. Finally, the next vector (45 degrees) represents low-angle light and is rendered as green.
Think of the colours of the ASET and Ideal-Scope as capturing overhead light as the sky (blue), with red as the high sun and green as the surrounding trees and horizon. (The schematic seen in Figure 7 is a simple 2D rendering.)
The arrows, therefore, represent the total amount of overhead light obscured by the viewer. There are four opposite sets of arrows on a well-cut round brilliant. This is touted by the jewellery industry as an asset, as these create a contrast with the rest of the facets, producing a desirable effect.
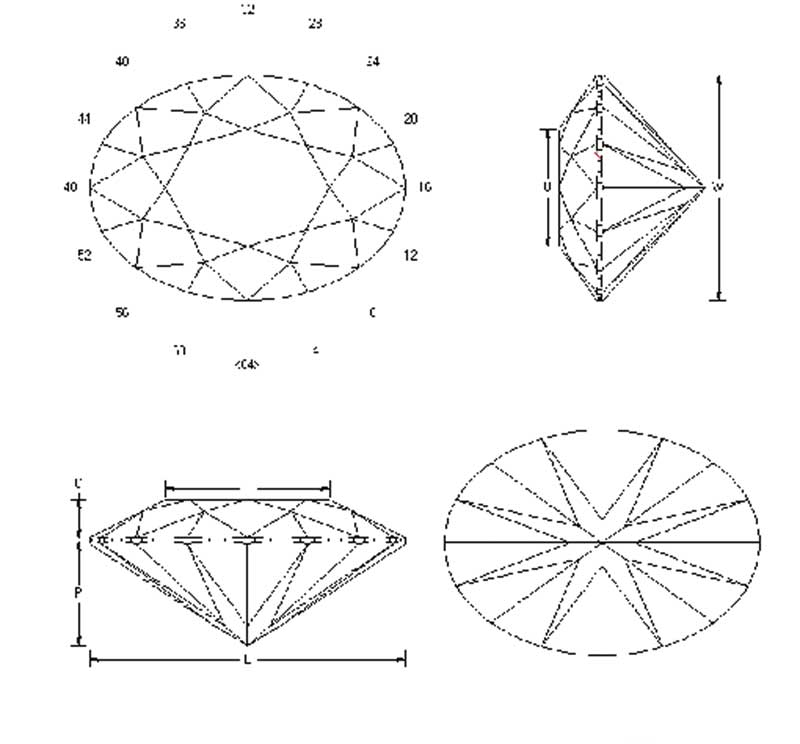
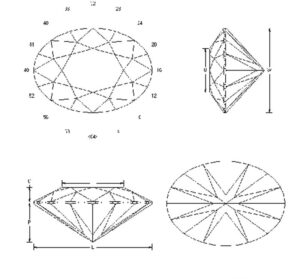
When applying the same angular and index criteria to oval, pear, and marquise-cut diamonds, we get dark centres referred to as ‘bow ties.’ This effect is considered very undesirable, as diamonds are normally bright. While we have a single bow tie in each of the fancies, however, no one ever refers to the eight arrows in a round brilliant as ‘four bow ties.’ Indeed, though this effect is one and the same, it is somehow considered desirable in the one cut but not in others.
Avoiding bow ties
Fancy-shaped diamonds could be cut according to traditional methods and exhibit distinctive bow ties. The presence of a bow tie is not a sign of poor workmanship, but, rather, poor design. A diamond could be cut to extreme perfection yet still have distinct bow ties.
There are several ways to eliminate bow ties:
- For traditional ovals: lower the pavilion angle (which may lead to crushed ice effect).
- For traditional ovals: increase the pavilion angle (which will compromise light return).
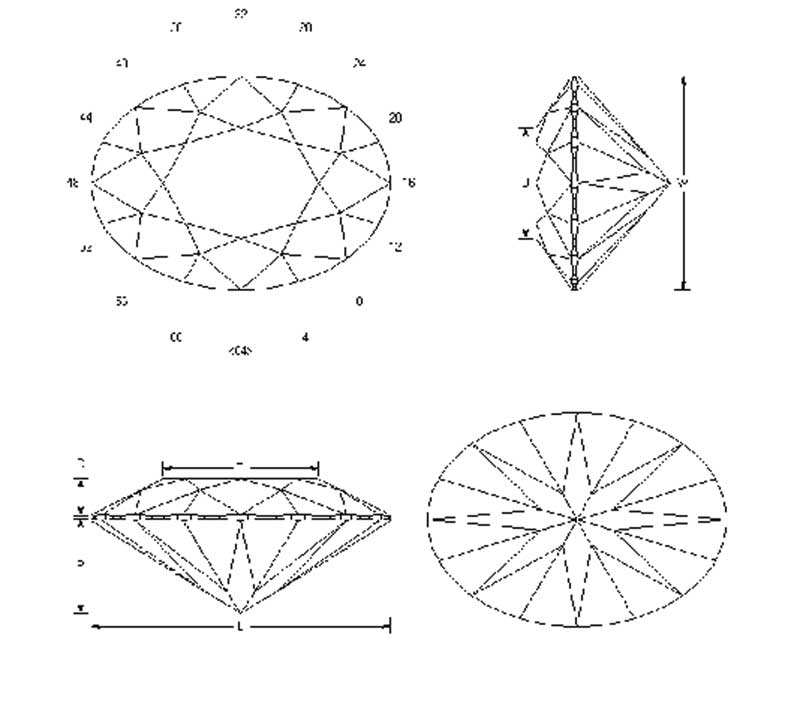
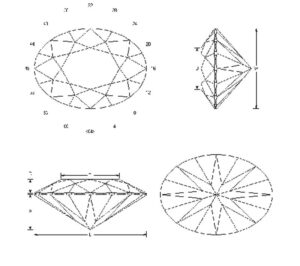
- Rotate the pavilion mains to line up with the star facets.
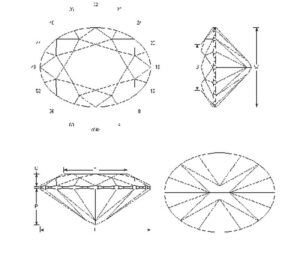
- Cut four pavilion mains to coincide with the wing facets, forming a French culet.
This applicable to pear and marquise cuts as well.
Additionally, off setting the main pavilion facets on oval, pear, and marquise-cut diamonds by aligning them with the indices of the star facets can result in fancies with no bow ties, along with overall stunning appearance and optimized light return.
A reflection of ‘us’
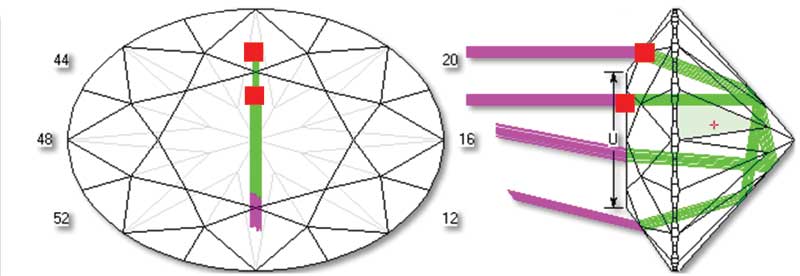
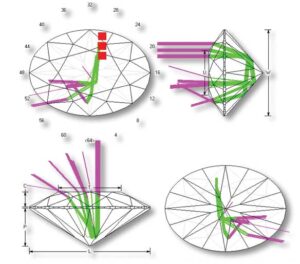
Diamond pavilion facets act as mirrors, reflecting whatever they ‘see.’ These do not only reflect light, but also images in its surroundings. One of the most significant ‘things’ the diamond reflect is you—the viewer. Thus, the facets (mirrors) that reflect substantially linear to your visual axis will reflect your face.
Facets that reflect oblique to the visual axis will not have this effect, as these are pointing elsewhere. The pavilion main facets in the oval depicted in Figure 11, for example, will reflect the viewer, resulting in the ‘bow tie’ phenomenon. (The red squares indicate where simulated light beams enter, as well as where they exit.) Meanwhile, Figure 12 shows how the lower girdle facets reflect images/light, oblique to the line of sight.
If the viewer is surrounded by light, the facets would reflect light away from the viewer. They will, therefore, not ‘see’ the viewer and would not be part of a bow tie, unless the cutter did not create enough radial or angular definition (i.e. dug out the lower girdle facets).
For this master diamond cutter, the rotated pavilion main depicted in Figure 9 is preferred, as this design allows for the easiest execution and best symmetry. The next best option would be the French culet (Figure 11). That said, while stones in this fashion can be beautiful, this author has also seen many poorly cut fancies in this category with terribly uneven girdles.
Of course, like many aspects of diamonds and gem-cutting, beauty is in the eye of the beholder.
 Master diamond cutter Mike Botha, RS, and his son, Evert Botha, RS, operate a diamond atelier in Prince Albert, Sask., specializing in designing, cutting, and polishing high-performance diamonds. For more information, visit masterdiamondcutters.com or siriusstardiamond.com.
Master diamond cutter Mike Botha, RS, and his son, Evert Botha, RS, operate a diamond atelier in Prince Albert, Sask., specializing in designing, cutting, and polishing high-performance diamonds. For more information, visit masterdiamondcutters.com or siriusstardiamond.com.